Generating random numbers in perl
What is a random number?
- You can't predict what it will be, even if you have been watching its source.
- You usually know the likely distribution, which is usually uniform.
Each bit in a uniform random sequence is independent and equally likely to be 0 or 1.
Equally distributed numbers are made by clumping together uniform random bits.
my @bits = (1, 0, 0, 1, 1);
my $int = oct('0b'. join('', @bits)); my $n = $int / 2 ** @bits;
print "bits: @bits int: $int n: $n\n";
bits: 1 0 0 1 1 int: 19 n: 0.59375
Bits are usually grouped in sets of 15, 31, or 48. More than 53 is pointless for ordinary floating numbers.
Non-uniform distributions
Other distributions are useful

but I am not going to talk about these.
Converting between various random distributions is not hard.
CPAN has, for example, Math::Random::Cauchy and
Math::Random::OO::Normal, which make different kinds of
bell curve.
Types of random number generators
Hardware vs Software
It is impossible to get true random numbers from software.
According to current understanding, some hardware generators
would remain unpredictable even if you knew everything.
Hardware generators are often slow and imperfectly uniform.
Often software is used to extend and regularise ("whiten") their
output.
Acceptable levels of randomness
"unpredictable" has different values, depending on what is to be
fooled. There are trade-offs between speed, inscrutability, and
algorithmic simplicity.
Software pseudo-random number generators
These can be classified into three categories:
Cryptographic generators
For Alice and Bob. There
should be no practical way of predicting their output.
Statistical generators
These ought to be indistinguishable from true random generators,
unless the use case is crafted to reverse the randomising algorithm.
Cryptographic generators would work for statistical purposes, but
are (supposedly) slower.
Toy Generators
Can baffle inattentive game players.
Perl's rand falls into the last category.
rand()
rand is perl's builtin pseudo-random number generating function.
By default it is defined in C as:
sub rand {
my $top = shift || 1.0;
$top * (libc_rand() & 32767) / 32768;
}
where:
-
libc_rand refers to libc's rand. It returns an integer between 0
and a number called RAND_MAX, which is usually 2**31, but is
allowed to be as low as 2**15.
- 32768 is 2 ** 15.
Problems with rand
You can't randomly select between 33,000 options.
But it is actually worse than it looks.
Libc's rand works like this:
my $random_state;
sub libc_rand {
$random_state = (1103515245 * $random_state + 12345) % (2**31);
}
but that won't actually work, because perl doesn't cope well with large integers. you can use bigint, or do this:
sub libc_rand {
use integer;
$random_state = (1103515245 * $random_state + 12345) & 0x7fffffff;
}
Linear Congruential Generators
The formula $new_state = ($a * $old_state + $c) % $m is called a "linear congruential generator"
or LCG.
If $a, $c, and $m are
carefully chosen, $random_state goes through every integer (modulo
$m), before starting again. This gives the libc generator a period
of 2**31, or 2,147,483,648.
If you plot its results on a line, they will spread out nicely.
If you group them into sets and plot them on a higher dimensional
graph, they end up lying on a few hyperplanes.
(To be more precise, At most (2**31) ** (1/n) hyperplanes).
Hyperplanes illustrated
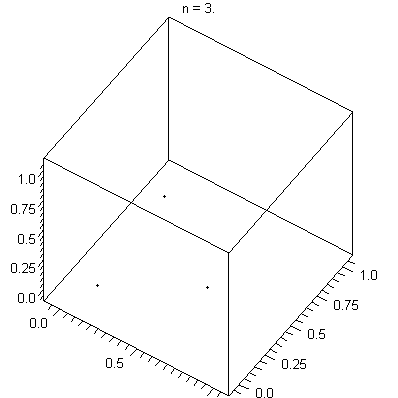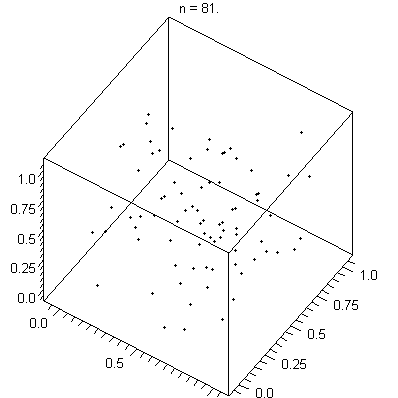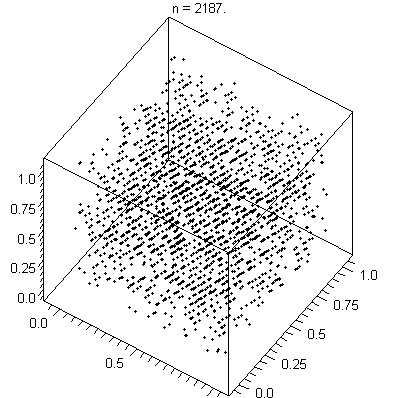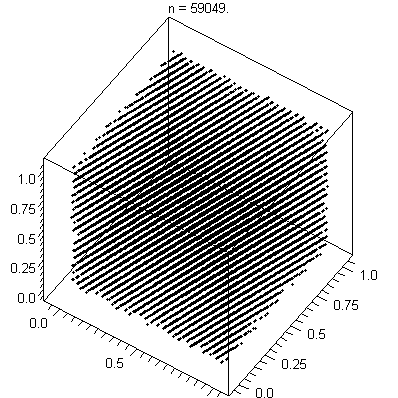
[image: wikpedia]
"We guarantee that each number is random individually, but we
don't guarantee that more than one of them is random." -- early LCG vendor.
Plotting points in multidimensional space is something you do all the time without knowing it.
Data::RandomPerson
Generates fake people with names, ages, titles, etc.
These are generated by 7 consecutive calls to rand(), which is
equivalent to plotting a point in a 7-dimensional hypercube.
The points lie on at most $period ** (1/7)
hyperplanes. On Linux that means 115 hyperplanes, on Windows,
4.
Data::RandomPerson could generate a few hundred trillion
possibilities, if the random number generator could
reach them.
LCG low order bits
for (1..2){
for (1..16){
printf "%3d", (libc_rand() & 1);
}
print "\n";
}
1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0
1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0
1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0
1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0
1 6 7 4 5 2 3 0 1 6 7 4 5 2 3 0
1 6 7 4 5 2 3 0 1 6 7 4 5 2 3 0
The low order bits are the least random.
LCG bit patterns, continued
my @r = map {libc_rand()}(1..64);
foreach my $s (0..5){
printf "\n%2d ", 1<< $s;
foreach (@r){
print $_ & 1<<$s ? 'x' : ' ';
}
}
1 x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
2 xx xx xx xx xx xx xx xx xx xx xx xx xx xx xx xx
4 xxxx xxxx xxxx xxxx xxxx xxxx xxxx xxxx
8 xxxx xxx x xxxx xxx x xxxx xxx x xxxx xxx x
16 xxx x xxxxx xx x x xxx xxx x xxxxx xx x x xxx
32 xx xx x x xxxxxx xxx x x xx x x x xxx xx x xx xx
Higher bits have less obvious patterns with longer periods. As they
are overlaid, the whole seems to get fairly random.
But only if you look from the top.
Perl's rand, recalled
By default perl's rand is defined in C as:
sub rand {
my $top = shift || 1.0;
$top * (libc_rand() & 32767) / 32768;
}
perl carefully discards the good bits.
On most systems the configure system will try to find a better solution.
Specifically, on Linux or BSD it will find a libc function called drand48.
drand48
Also a linear congruential generator, using different numbers:
sub libc_rand48 {
use bigint;
$random_state = (25_214_903_917 * $random_state + 11) % (2**48);
}
sub libc_drand48 {
return libc_rand48() / (2**48);
}
so perl's rand, on a properly configured BSD or Linux system will be:
sub rand {
(shift || 1.0) * libc_drand48();
}
drand48
The period is greater (281 trillion), and all the best bits are used.
However it is still a linear congruential generator, so it will still
lay its points on hyperplanes, and it will always have bad
characteristics in the low bits.
![[image showing drand48 lattice]](img140.gif) If my deep linking is working, this should be a picture of pairs of drand48 values plotted in two dimensions.
If my deep linking is working, this should be a picture of pairs of drand48 values plotted in two dimensions.
If it isn't, please imagine a close up view of a diagonal pinstripe covering the plane.
source:
Karl Entacher, University of Salzburg.
Does it matter?
yes, sometimes.
- Bad distribution matters, obviously
- dimensional correlations are pernicious
- Periodicity can matter, depending how you look at it
Clocking RNG's (at 16M numbers per second)
period cycle
2**15 2 milliseconds
2**24 1 second
2**31 2 minutes
2**48 6 months
2**64 34877 years
2**19937 "inf" (c. 2 ** 19888) years
While 64 bits is enough for "never repeats" in continuous use, it
is possible to accidentally repeat a sequence by
re-starting from nearby points in the cycle.
Theoretical need for large period: case study
You are building an online poker empire, or a secret machine to
ruin an online poker empire.
The pack can be shuffled 52! ways (52 * 51 * 50 * 49...).
A random number generator can shuffle a pack into no more
states than it has itself (and easily fewer).
sub fact{
my $a = 1;
for (1..shift){
$a *= $_;
}
$a;
}
fact(52); 2** 48;
rand cannot reach most shufflings.
How many games of Microsoft Solitaire do you need to play before you play the same game twice?
Microsoft's libc generator has a period of 32768.
my $STATES = 32767;
my $tries = 0;
my $p = 1.0;
while ($p > 0.5){
$p *= (($STATES - $tries) / $STATES);
$tries++;
}
print "$p $tries\n";
On average, After 214 games you will have played one of
them twice (or sooner, if Microsoft were not careful in their use
of the generator).
You could get around this by gathering randomness from elsewhere
and/or collecting state -- in other words, by writing another RNG on top.
A contrived example calling for a large period RNG
(skip this 3 slide digression)
You have a large database which you hope indexes people. You
want to conduct a survey to see whether it actually refers to cats and
dogs.
Suppose you have 2.8 million entries. The number of combinations
of n individuals is 2800000! / (28000000 - n)! / n! .
For relatively small n, this is close to 2800000 ** n / n!.
A reasonable sample might be 500 people.
print 2800000 ** 500 / fact(500);
Pseudo-random number generators tend not to have infinite periods.
Big numbers
To deal with big numbers in perl, you need to use
big(int|num|rat), or the more specific use
Math::Big(Int|Num|Rat), or to use logarithms. I didn't know
about the pragma versions when I did these calculations, so
logarithms seemed easiest.
sub log2 {
return log(shift) / log(2);
}
my $pop = log2(2800000); my $permutations = $pop * 500;
sub factlog2 {
my $a = 0;
for (1..shift){
$a += log2($_);
}
$a;
}
my $combinations = $permutations - factlog2(500);
You need a generator with a period of over 2 ** 6942
to randomly select from all possible sets of 500.
With a good libc rand (period 2 ** 48), you would be able to pick
any combination of 2 people (2 ** 41.8), but not of 3 (2 ** 61.7).
This probably has no practical significance.
Shuffling calculations using logarithms
printf "%f\n", factlog2(52);
sub max_shuffle{
my $bits = shift;
my $i = 0;
while($bits > 0){
$bits -= log2(++$i);
}
return $i - 1;
}
foreach (15, 31, 48, 226, 9689, 19937){
printf "%6d bits can shuffle %4d items\n", $_, max_shuffle($_);
}
15 bits can shuffle 7 items
31 bits can shuffle 12 items
48 bits can shuffle 16 items
226 bits can shuffle 52 items
9689 bits can shuffle 1115 items
19937 bits can shuffle 2080 items
Millions have been lost in Melbourne Cup
sweepstakes organised in Excel.
Some RNG families
Random number generators are grouped into overlapping families.
{$x = ($a * $x + $c) % $m; return $x / $m}
{$x[$i] = ($a1 * $x[$i-1] + $a2 * $x[$i-2] + $a3 * $x[$i-3] ) % $m; return $x[$i]/$m }
lfib($m, $r, $k, $op) => {$x[$i] = ($x[$i-$r] $op $x[$i-$k] ) % $m};
lfib(2**48, 607, 273, '+');
lfib(2**64, 1279, 861, '*');
{$x[$i] = $x[$i-$r] ^ $x[$i-$k]; return $x[$i]/$m}
Lagged Fibonacci Generator Generator
sub lfib{
my ($m, $r, $k, $op, $seed) = @_;
my (@x, $i);
srand($seed ||time); for (0 .. $r){
push @x, int(rand($m));
}
my $fn = "sub {
\$i = (\$i + 1) % $r;
\$x[\$i] = (\$x[\$i] $op \$x[(\$i-$k) % $r]) % $m;
(shift || 1.0) * \$x[\$i] / $m;
}\n";
return eval($fn);
}
$rand = lfib(2**48, 607, 273, '+'); $rand2 = lfib(2**64, 1279, 861, '*');
print &$rand(100) . "\n" . &$rand2() ."\n";
54.6312745966894
0.0627432743424777
Maybe this should use bignum, but it seems to work without.
Example statistical generator: gfsr4 or Ziff98
Four tap Generalised Feedback Shift Register, designed by Robert M. Ziff in 1998.
@r = <long list of numbers>;
$n = <index>;
A, B, C, D = <special constants>.
$n++;
$r[$n] = $r[$n-A] ^ $r[$n-B] ^ $r[$n-C] ^ $r[$n-D];
Each bit in the new number depends on whether there are an even
or odd number of ones in the four previously generated numbers.
gfsr4 / Ziff98
my $random_state;
sub srand{
my $seed = shift || time || 4357;
my @a = ();
for (1..10000){
use integer;
push @a, $seed & 0x7fffffff;
$seed *= 69069;
}
$random_state = {
offset => 0,
array => \@a
}
}
sub rand{
my $range = shift || 1.0;
::srand() unless defined $random_state;
$random_state->{offset} = ($random_state->{offset} + 1) % 10000;
my $off = $random_state->{offset};
my $a = $random_state->{array};
$$a[$off] = ($$a[($off - 471) % 10000] ^
$$a[($off - 1586) % 10000] ^
$$a[($off - 6988) % 10000] ^
$$a[($off - 9689) % 10000]);
return $$a[$off] * $range / (2**31);
}
Qualities of gfsr4
- Period of 2 ** 9689 - 1
- Each bit is independent of the others (31 1-bit generators
running in parallel).
- Nice distribution according to most, but not all, tests.
- Very fast, except when written by me, in perl.
- Somewhat wasteful of space.
- Its state space contains degenerate regions (each bit's cycle has long stretches of zeros).
Mersenne Twister, or MT19937
By Makoto Matsumoto and Takuji Nishimura, with three versions
between 1997 and 2002. Quicker, allegedly better, SIMD version released
2006.
- Period of 2 ** 19937 - 1
- equi-distributed "up to 623 dimensions"
- fast
- its state space contains degenerate regions
- efficient storage of state (624 32 bit integers)
There are CPAN modules that override rand.
use Math::Random::MT qw(rand);
use Math::Random::MT::Auto qw(rand);
The second one works faster, but is fiddlier to install. Both
are partly implemented in C.
Works like a GFSR, but twisted and tempered using a clever
sequence of shifts and xors against itself and magic numbers, which
are described in terms of matrices.
Approximate implementation of MT19937
my $random_state;
sub srand{
use integer;
my @state = (shift || time || 5489);
for (1 .. 624){
push @state, (1812433253 * ($state[$_ - 1] ^ ($state[$_ - 1] >> 30)) + $_);
}
$random_state = {
state => \@state,
offset => 624
}
}
sub twist{
use integer;
my ($u, $v) = @_;
my $t = (($u & 0x80000000) | ($v & 0x7fffffff)) >> 1;
my $s = ($v & 1) ? 0x9908b0df : 0;
return $t ^ $s;
}
sub temper{
use integer;
my $y = shift;
$y ^= ($y >> 11);
$y ^= ($y << 7) & 0x9d2c5680;
$y ^= ($y << 15) & 0xefc60000;
$y ^= ($y >> 18);
return $y;
}
sub rand{
use integer;
my $scale = shift || 1.0;
::srand() unless defined $random_state;
if ($random_state->{offset} > 623){
my $state = $random_state->{state};
for (0 .. 623){
$$state[$_] = ($$state[($_ + 397) % 624] ^
twist($$state[$_], $$state[($_ + 1) % 624]));
}
$random_state->{offset} = 0;
}
my $y = temper($random_state->{state}->[$random_state->{offset}]);
$random_state->{offset}++;
{
no integer;
return $y * $scale / 2**31;
}
}
Cryptographic random number generators
There are several variations.
A common method is to use a hash function on a counter, or
recursively upon itself. Or perhaps both, like so:
use Digest;
my $random_state;
sub srand{
my $seed = shift || ("use a better default than this " . time);
$random_state = {
digest => new Digest ("SHA-256"),
counter => 0,
waiting => [],
prev => $seed
};
}
sub rand{
my $range = shift || 1.0;
::srand() unless defined $random_state;
if (! @{$random_state->{waiting}}){
$random_state->{digest}->reset();
$random_state->{digest}->add("string together your entropy, state, etc" .
$random_state->{counter} ++ .
$random_state->{prev});
$random_state->{prev} = $random_state->{digest}->digest();
my @ints = unpack("L*", $random_state->{prev}); $random_state->{waiting} = \@ints;
}
my $int = shift @{$random_state->{waiting}};
return $range * $int / 2**32;
}
Crypt::OpenSSL::Random
use Crypt::OpenSSL::Random;
my $random_state;
sub srand{
use integer;
my $seed = shift || time || 5489;
while (! Crypt::OpenSSL::Random::random_seed(pack('j', $seed))){
$seed = (1103515245 * $seed + 12345);
}
$random_state = [];
}
sub rand{
my $range = shift || 1.0;
::srand() unless $random_state;
if (! @$random_state){
my $bytes = Crypt::OpenSSL::Random::random_bytes(256);
@$random_state = unpack("L*", $bytes);
}
my $int = shift @$random_state;
return $range * $int / 2**32;
}
AES is allegedly good and quick. ISSAC claims to be faster, and
the new generation at http://www.ecrypt.eu.org/stream/
consider themselves to be faster and better still.
Other languages
Ruby Mersenne Twister (not the same Matsumoto)
Python Mersenne Twister
PHP both (rand and mt_rand)
Visual Basic $r = ($r * 1140671485 + 12820163) % (2 ** 24)
(BETTER than perl on windows)
javascript (moz) 48 bit linear congruential generator
(like perl on BSD or Linux)
java 48 bit linear congruential generator
(fiddled with but not improved)
lua libc (31 bit, except on windows)
C libc (or Gnu Scientific Library and others)
mysql {$a=($a*3 + $b) % $m; $b=($a + $b + 33) % $m; $a/$m}
postgresql libc drand48 (with windows port)
Perl 6 ? (pugs uses libc and 'Math::Random::Kiss')
Speed and conclusions.
1 million numbers (Athlon XP 2800+, Debian Sid, perl 5.8.8)
raw minus overhead
perl Mersenne Twister 7.691 7.451
gfsr4 5.177 4.937
sha-256 5.079 4.839
Math::Random::MT 3.360 3.120
Crypt::OpenSSL::Random 2.817 2.577
lfib(2**48, 607, 273, '+') 2.374 2.134 ('use bignum': c.1300)
Math::Random::MT::Auto 0.972 0.732
system rand 0.361 0.121
none 0.240 0.0
If Math::Random::MT::Auto is too slow, your program is probably too
reliant on random numbers to not use it.
Crypt::OpenSSL::Random is less predictable and not really slow.
There are other modules I haven't tested.
If you are using PDL, try PDL::GSL::RNG.
Rolling your own is fun, easy, and not recommended.
Resources
CPAN
Search for "random" or "rand", or browse the /Security area
for Crypt::* and Digest:: modules.
Math::Random::MT::Auto
Math::Random::MT
Crypt::OpenSSL:Random
PDL::GSL::RNG #comes with PDL
Math::TrulyRandom #interface to hardware
Data::Entropy
Bundle::Math::Random #
Other stuff
the end (+code)
Most of the code seen in these slides (and some more besides) is in one of these scripts:
These are illustrative only, and should not be trusted as random number generators.


![[image showing drand48 lattice]](img140.gif) If my deep linking is working, this should be a picture of pairs of drand48 values plotted in two dimensions.
If my deep linking is working, this should be a picture of pairs of drand48 values plotted in two dimensions.