Each bit in a uniform random sequence is independent and equally likely to be 0 or 1.
Equally distributed numbers are made by clumping together uniform random bits.
# translating random bits to a fraction between 0 and 1 my @bits = (1, 0, 0, 1, 1); my $int = oct('0b'. join('', @bits)); #yes, oct my $n = $int / 2 ** @bits; # $n is the binary fraction 0.10011 print "bits: @bits int: $int n: $n\n"; bits: 1 0 0 1 1 int: 19 n: 0.59375
Bits are usually grouped in sets of 15, 31, or 48. More than 53 is pointless for ordinary floating numbers.
Other distributions are useful
but I am not going to talk about these.
Converting between various random distributions is not hard.
CPAN has, for example, Math::Random::Cauchy and
Math::Random::OO::Normal, which make different kinds of
bell curve.
It is impossible to get true random numbers from software.
According to current understanding, some hardware generators would remain unpredictable even if you knew everything.
Hardware generators are often slow and imperfectly uniform. Often software is used to extend and regularise ("whiten") their output.
"unpredictable" has different values, depending on what is to be fooled. There are trade-offs between speed, inscrutability, and algorithmic simplicity.
These can be classified into three categories:
For Alice and Bob. There should be no practical way of predicting their output.
These ought to be indistinguishable from true random generators, unless the use case is crafted to reverse the randomising algorithm. Cryptographic generators would work for statistical purposes, but are (supposedly) slower.
Can baffle inattentive game players.
Perl's rand falls into the last category.
rand is perl's builtin pseudo-random number generating function.
By default it is defined in C as:
sub rand { my $top = shift || 1.0; $top * (libc_rand() & 32767) / 32768; }
where:
libc_rand refers to libc's rand. It returns an integer between 0
and a number called RAND_MAX, which is usually 2**31, but is
allowed to be as low as 2**15.
You can't randomly select between 33,000 options.
But it is actually worse than it looks. Libc's rand works like this:
my $random_state; #an integer, first set by srand() sub libc_rand { $random_state = (1103515245 * $random_state + 12345) % (2**31); }
but that won't actually work, because perl doesn't cope well with large integers. you can use bigint, or do this:
# 'use integer' makes integer maths modulus 2**32 sub libc_rand { use integer; $random_state = (1103515245 * $random_state + 12345) & 0x7fffffff; }
The formula $new_state = ($a * $old_state + $c) % $m is called a "linear congruential generator"
or LCG.
If $a, $c, and $m are carefully chosen, $random_state goes through every integer (modulo $m), before starting again. This gives the libc generator a period of 2**31, or 2,147,483,648.
If you plot its results on a line, they will spread out nicely.
If you group them into sets and plot them on a higher dimensional graph, they end up lying on a few hyperplanes.
(To be more precise, At most (2**31) ** (1/n) hyperplanes).
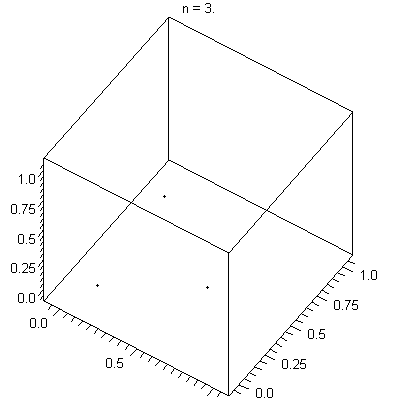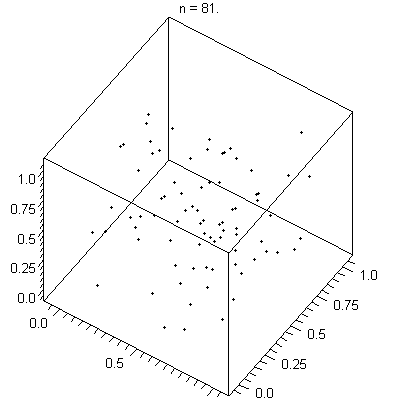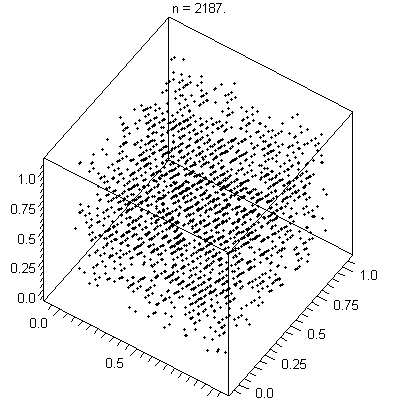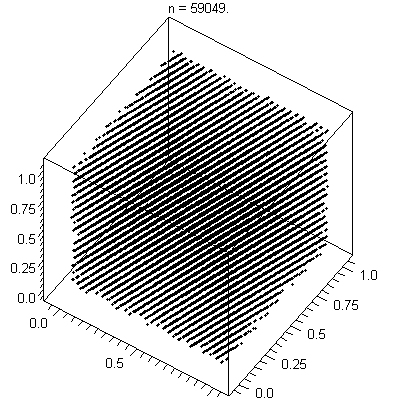
[image: wikpedia]
"We guarantee that each number is random individually, but we don't guarantee that more than one of them is random." -- early LCG vendor.
Plotting points in multidimensional space is something you do all the time without knowing it.
Generates fake people with names, ages, titles, etc.
These are generated by 7 consecutive calls to rand(), which is equivalent to plotting a point in a 7-dimensional hypercube.
The points lie on at most $period ** (1/7)
hyperplanes. On Linux that means 115 hyperplanes, on Windows,
4.
Data::RandomPerson could generate a few hundred trillion possibilities, if the random number generator could reach them.
for (1..2){ for (1..16){ printf "%3d", (libc_rand() & 1); } print "\n"; }
1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0
# libc_rand() & 3
1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0
1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0
# libc_rand() & 7
1 6 7 4 5 2 3 0 1 6 7 4 5 2 3 0
1 6 7 4 5 2 3 0 1 6 7 4 5 2 3 0
The low order bits are the least random.
my @r = map {libc_rand()}(1..64); foreach my $s (0..5){ printf "\n%2d ", 1<< $s; foreach (@r){ print $_ & 1<<$s ? 'x' : ' '; } }
1 x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x 2 xx xx xx xx xx xx xx xx xx xx xx xx xx xx xx xx 4 xxxx xxxx xxxx xxxx xxxx xxxx xxxx xxxx 8 xxxx xxx x xxxx xxx x xxxx xxx x xxxx xxx x 16 xxx x xxxxx xx x x xxx xxx x xxxxx xx x x xxx 32 xx xx x x xxxxxx xxx x x xx x x x xxx xx x xx xx
Higher bits have less obvious patterns with longer periods. As they are overlaid, the whole seems to get fairly random.
But only if you look from the top.
By default perl's rand is defined in C as:
sub rand { my $top = shift || 1.0; $top * (libc_rand() & 32767) / 32768; }
perl carefully discards the good bits.
On most systems the configure system will try to find a better solution.
Specifically, on Linux or BSD it will find a libc function called drand48.
Also a linear congruential generator, using different numbers:
sub libc_rand48 { use bigint; #because the numbers are > 32 bit. $random_state = (25_214_903_917 * $random_state + 11) % (2**48); } #libc converts it to floating point. sub libc_drand48 { return libc_rand48() / (2**48); }
so perl's rand, on a properly configured BSD or Linux system will be:
sub rand { (shift || 1.0) * libc_drand48(); }
The period is greater (281 trillion), and all the best bits are used.
However it is still a linear congruential generator, so it will still lay its points on hyperplanes, and it will always have bad characteristics in the low bits.
![[image showing drand48 lattice]](img140.gif)
If my deep linking is working, this should be a picture of pairs of drand48 values plotted in two dimensions.
If it isn't, please imagine a close up view of a diagonal pinstripe covering the plane.
source: Karl Entacher, University of Salzburg.
yes, sometimes.
period cycle 2**15 2 milliseconds 2**24 1 second 2**31 2 minutes 2**48 6 months 2**64 34877 years 2**19937 "inf" (c. 2 ** 19888) years
While 64 bits is enough for "never repeats" in continuous use, it is possible to accidentally repeat a sequence by re-starting from nearby points in the cycle.
You are building an online poker empire, or a secret machine to ruin an online poker empire.
The pack can be shuffled 52! ways (52 * 51 * 50 * 49...).
A random number generator can shuffle a pack into no more states than it has itself (and easily fewer).
sub fact{ my $a = 1; for (1..shift){ $a *= $_; } $a; } # inexact, due to perl's numerical oddities. fact(52); # 80658175170943876845634591553351679477960544579306048386139594686464.0 2** 48; # 281474976710656
rand cannot reach most shufflings.
Microsoft's libc generator has a period of 32768.
my $STATES = 32767; my $tries = 0; my $p = 1.0; while ($p > 0.5){ $p *= (($STATES - $tries) / $STATES); $tries++; } print "$p $tries\n"; # prints 0.498045943609997 214
On average, After 214 games you will have played one of them twice (or sooner, if Microsoft were not careful in their use of the generator).
You could get around this by gathering randomness from elsewhere and/or collecting state -- in other words, by writing another RNG on top.
(skip this 3 slide digression)
You have a large database which you hope indexes people. You want to conduct a survey to see whether it actually refers to cats and dogs.
Suppose you have 2.8 million entries. The number of combinations
of n individuals is 2800000! / (28000000 - n)! / n! .
For relatively small n, this is close to 2800000 ** n / n!.
A reasonable sample might be 500 people.
print 2800000 ** 500 / fact(500); # "inf"
Pseudo-random number generators tend not to have infinite periods.
To deal with big numbers in perl, you need to use
big(int|num|rat), or the more specific use
Math::Big(Int|Num|Rat), or to use logarithms. I didn't know
about the pragma versions when I did these calculations, so
logarithms seemed easiest.
sub log2 { return log(shift) / log(2); } my $pop = log2(2800000); # 21.417 my $permutations = $pop * 500; #10708.498 sub factlog2 { my $a = 0; for (1..shift){ $a += log2($_); } $a; } my $combinations = $permutations - factlog2(500); # 6941.1
You need a generator with a period of over 2 ** 6942 to randomly select from all possible sets of 500.
With a good libc rand (period 2 ** 48), you would be able to pick any combination of 2 people (2 ** 41.8), but not of 3 (2 ** 61.7).
This probably has no practical significance.
printf "%f\n", factlog2(52); # 225.58 ; 2**225.58 == fact(52) sub max_shuffle{ my $bits = shift; my $i = 0; while($bits > 0){ $bits -= log2(++$i); } return $i - 1; } foreach (15, 31, 48, 226, 9689, 19937){ printf "%6d bits can shuffle %4d items\n", $_, max_shuffle($_); }
15 bits can shuffle 7 items
31 bits can shuffle 12 items
48 bits can shuffle 16 items
226 bits can shuffle 52 items
9689 bits can shuffle 1115 items
19937 bits can shuffle 2080 items
Millions have been lost in Melbourne Cup sweepstakes organised in Excel.
Random number generators are grouped into overlapping families.
#Linear Congruential Generators {$x = ($a * $x + $c) % $m; return $x / $m} #often sub-categorised into "bad" and "awful", or by whether $m is a power of 2. #Multiple Recursive Generator # these can be good. $a*'s are usually if not always 1 or 0 {$x[$i] = ($a1 * $x[$i-1] + $a2 * $x[$i-2] + $a3 * $x[$i-3] # and so on... ) % $m; return $x[$i]/$m } #Lagged Fibonacci # many others are special cases of this. # and many of these are special cases of others. lfib($m, $r, $k, $op) => {$x[$i] = ($x[$i-$r] $op $x[$i-$k] ) % $m}; lfib(2**48, 607, 273, '+'); #has period of 2**638 #multiplicative lagged Fibonacci generators do quite well lfib(2**64, 1279, 861, '*'); # period of 2**1340, passes tests, quick. #General Feedback Shift Register {$x[$i] = $x[$i-$r] ^ $x[$i-$k]; return $x[$i]/$m} # an LFib with xor operator, which makes the modulus redundant #Hash based RNGs -- repetitive use of cryptographic hashes. #Combined RNGs. By combining different families, you can get better results. or not.
sub lfib{ my ($m, $r, $k, $op, $seed) = @_; my (@x, $i); srand($seed ||time); #initialise state with rand for (0 .. $r){ push @x, int(rand($m)); } my $fn = "sub { \$i = (\$i + 1) % $r; \$x[\$i] = (\$x[\$i] $op \$x[(\$i-$k) % $r]) % $m; (shift || 1.0) * \$x[\$i] / $m; }\n"; return eval($fn); } $rand = lfib(2**48, 607, 273, '+'); #additive LFib, period 2 ** 638 $rand2 = lfib(2**64, 1279, 861, '*');#multiplicative LFib, period 2 ** 1340 print &$rand(100) . "\n" . &$rand2() ."\n"; 54.6312745966894 0.0627432743424777
Maybe this should use bignum, but it seems to work without.
Four tap Generalised Feedback Shift Register, designed by Robert M. Ziff in 1998.
@r = <long list of numbers>; $n = <index>; A, B, C, D = <special constants>. $n++; $r[$n] = $r[$n-A] ^ $r[$n-B] ^ $r[$n-C] ^ $r[$n-D]; # @r can wrap.
Each bit in the new number depends on whether there are an even or odd number of ones in the four previously generated numbers.
my $random_state; sub srand{ my $seed = shift || time || 4357; my @a = (); for (1..10000){ use integer; push @a, $seed & 0x7fffffff; $seed *= 69069; } $random_state = { offset => 0, array => \@a } } sub rand{ my $range = shift || 1.0; ::srand() unless defined $random_state; $random_state->{offset} = ($random_state->{offset} + 1) % 10000; my $off = $random_state->{offset}; my $a = $random_state->{array}; $$a[$off] = ($$a[($off - 471) % 10000] ^ $$a[($off - 1586) % 10000] ^ $$a[($off - 6988) % 10000] ^ $$a[($off - 9689) % 10000]); return $$a[$off] * $range / (2**31); }
By Makoto Matsumoto and Takuji Nishimura, with three versions between 1997 and 2002. Quicker, allegedly better, SIMD version released 2006.
There are CPAN modules that override rand.
use Math::Random::MT qw(rand); use Math::Random::MT::Auto qw(rand);
The second one works faster, but is fiddlier to install. Both are partly implemented in C.
Works like a GFSR, but twisted and tempered using a clever sequence of shifts and xors against itself and magic numbers, which are described in terms of matrices.
my $random_state; sub srand{ use integer; my @state = (shift || time || 5489); # initialise with a lesser RNG for (1 .. 624){ push @state, (1812433253 * ($state[$_ - 1] ^ ($state[$_ - 1] >> 30)) + $_); } $random_state = { state => \@state, offset => 624 } } sub twist{ use integer; my ($u, $v) = @_; my $t = (($u & 0x80000000) | ($v & 0x7fffffff)) >> 1; my $s = ($v & 1) ? 0x9908b0df : 0; return $t ^ $s; } sub temper{ use integer; my $y = shift; $y ^= ($y >> 11); $y ^= ($y << 7) & 0x9d2c5680; $y ^= ($y << 15) & 0xefc60000; $y ^= ($y >> 18); return $y; } sub rand{ use integer; my $scale = shift || 1.0; ::srand() unless defined $random_state; if ($random_state->{offset} > 623){ my $state = $random_state->{state}; for (0 .. 623){ $$state[$_] = ($$state[($_ + 397) % 624] ^ twist($$state[$_], $$state[($_ + 1) % 624])); } $random_state->{offset} = 0; } my $y = temper($random_state->{state}->[$random_state->{offset}]); #$y >>= 1; #for 31 bit perl int $random_state->{offset}++; { no integer; return $y * $scale / 2**31; } }
There are several variations. A common method is to use a hash function on a counter, or recursively upon itself. Or perhaps both, like so:
use Digest; my $random_state; sub srand{ my $seed = shift || ("use a better default than this " . time); $random_state = { digest => new Digest ("SHA-256"), counter => 0, waiting => [], prev => $seed }; } sub rand{ my $range = shift || 1.0; ::srand() unless defined $random_state; if (! @{$random_state->{waiting}}){ $random_state->{digest}->reset(); $random_state->{digest}->add("string together your entropy, state, etc" . $random_state->{counter} ++ . $random_state->{prev}); $random_state->{prev} = $random_state->{digest}->digest(); my @ints = unpack("L*", $random_state->{prev}); # 32 bit unsigned integers $random_state->{waiting} = \@ints; } my $int = shift @{$random_state->{waiting}}; return $range * $int / 2**32; }
use Crypt::OpenSSL::Random; my $random_state; sub srand{ use integer; my $seed = shift || time || 5489; #don't really do this while (! Crypt::OpenSSL::Random::random_seed(pack('j', $seed))){ $seed = (1103515245 * $seed + 12345); } $random_state = []; } sub rand{ my $range = shift || 1.0; ::srand() unless $random_state; if (! @$random_state){ my $bytes = Crypt::OpenSSL::Random::random_bytes(256); @$random_state = unpack("L*", $bytes); } my $int = shift @$random_state; return $range * $int / 2**32; }
AES is allegedly good and quick. ISSAC claims to be faster, and the new generation at http://www.ecrypt.eu.org/stream/ consider themselves to be faster and better still.
Ruby Mersenne Twister (not the same Matsumoto)
Python Mersenne Twister
PHP both (rand and mt_rand)
Visual Basic $r = ($r * 1140671485 + 12820163) % (2 ** 24)
(BETTER than perl on windows)
javascript (moz) 48 bit linear congruential generator
(like perl on BSD or Linux)
java 48 bit linear congruential generator
(fiddled with but not improved)
lua libc (31 bit, except on windows)
C libc (or Gnu Scientific Library and others)
mysql {$a=($a*3 + $b) % $m; $b=($a + $b + 33) % $m; $a/$m} #$m=2**30-1
postgresql libc drand48 (with windows port)
Perl 6 ? (pugs uses libc and 'Math::Random::Kiss')
1 million numbers (Athlon XP 2800+, Debian Sid, perl 5.8.8)
raw minus overhead
perl Mersenne Twister 7.691 7.451
gfsr4 5.177 4.937
sha-256 5.079 4.839
Math::Random::MT 3.360 3.120
Crypt::OpenSSL::Random 2.817 2.577
lfib(2**48, 607, 273, '+') 2.374 2.134 ('use bignum': c.1300)
Math::Random::MT::Auto 0.972 0.732
system rand 0.361 0.121
none 0.240 0.0
If Math::Random::MT::Auto is too slow, your program is probably too
reliant on random numbers to not use it.
Crypt::OpenSSL::Random is less predictable and not really slow.
There are other modules I haven't tested.
If you are using PDL, try PDL::GSL::RNG.
Rolling your own is fun, easy, and not recommended.
Search for "random" or "rand", or browse the /Security area
for Crypt::* and Digest:: modules.
Math::Random::MT::Auto Math::Random::MT Crypt::OpenSSL:Random PDL::GSL::RNG #comes with PDL Math::TrulyRandom #interface to hardware Data::Entropy Bundle::Math::Random #
Most of the code seen in these slides (and some more besides) is in one of these scripts:
These are illustrative only, and should not be trusted as random number generators.